Have you ever wondered how floating point operations are actually represented on a computer? No? Me neither 🙂 However I have been reading a book called ‘Mathematics and Physics for Programmers’ by Danny Kodicek and the first chapter covers this. For one of the exercises it recommends writing code to carry out addition, subtraction, multiplication and division of IEEE floating point numbers that are represented as binary values. This blog post is the first in a two-part series that describes my implementation of those operations using STL strings.
Representing a floating point value as a binary value
According to the IEEE 754 standard, single precision represents a floating point value that occupies 32 bits / 4 bytes and double precision represents a floating point value that occupies 64 bits / 8 bytes. They are represented as the float and double POD types in C++ respectively. I used the float type in the code accompanying these posts. A single precision binary floating point format consists of 1 sign bit followed by 8 exponent bits and finally 23 mantissa bits. The sign bit describes whether the value is positive (0) or negative (1). The exponent describes the position of the decimal point and the mantissa contains the value. As the significand (most significant bit) of the mantissa is always 1 it is ignored when storing the value (it is implicit during calculations), therefore allowing for 24 bits of precision.
Below is the binary representation of 12.125:
In order to calculate the mantissa you calculate both the integer and fractional parts separately.
This involves converting the value 12 from base 10 to base 2
![\[1 \times 2^3 + 1 \times 2^2 + 0 \times 2^1 + 0 \times 2^0 = 1100\]](https://www.eoinoflynn.com/wp-content/ql-cache/quicklatex.com-1a1f8d7dc53a71bcb7f5d10829dcadde_l3.png "Rendered by QuickLaTeX.com")
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
string convert_base(size_t value, const size_t currentBase, const size_t wantedBase) { stringstream resultSS; const auto useLetters = (wantedBase > 10); // Convert value to wantedBase while (value >= wantedBase) { remainder = value % wantedBase; value = ((value - remainder) / wantedBase); resultSS << ((useLetters && remainder > 9) ? static_cast<char>(A + remainder - 10) : remainder); } resultSS << ((useLetters && value > 9) ? static_cast<char>(A + value - 10) : value ); auto number = resultSS.str(); // Reverse the order of the characters as the conversion above places the // characters in ascending order from left to right in the stringstream StringManipulation::reverseString(number); return number; } |
The method for converting the fractional part from base 10 to base 2 is slightly different.
first digit = 0.125 * 2 = 0.25; Integer part is 0 so digit is 0; carry 0.25
second digit = 0.25 * 2 = 0.5; Integer part is 0 so digit is 0; carry 0.5
third digit = 0.5 * 2 = 1.0; Integer part is 1 so digit is 1; Subtract 1.0 from result and carry remainder 1.0 – 1.0 = 0
fourth digit = 0; Stop and ignore
![\[0.125 = 001\]](https://www.eoinoflynn.com/wp-content/ql-cache/quicklatex.com-198a2aaa0178f41db05ab6f8dd84414f_l3.png "Rendered by QuickLaTeX.com")
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
string convertFractionalPartToBinary(const float value, const size_t allowedNumBits) { string fractionalPart(""); auto remainder = abs(value) - maths::floor(abs(value)); // Iterate until we reach 0 or the until the precision limit is reached for the mantissa while (remainder > 0.0 && fractionalPart.length() <= allowedNumBits) { remainder *= 2.0f; // base 2 for binary auto digit = maths::floor(remainder); fractionalPart.append(to_string(digit)); remainder -= digit; } return fractionalPart; } |
We add 127 to the exponent to allow us to represent negative numbers. Therefore the value of the exponent is in the range -128 -> 127
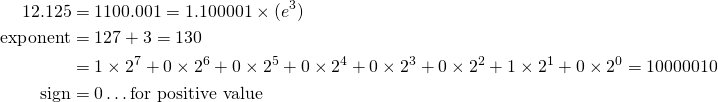
Mathematical Operation Setup
For addition, subtraction and multiplication, extracting the integer and fractional parts of the IEEE binary float in order to carry out the operations on each part individually simplifies the logic. For the integer parts the right hand side of the values need to align, whereas for the fractional parts the left hand side needs to align. For division the denominator is converted to a whole integer and there is no fractional part to worry about.
Addition
For binary addition, the rules are: 0 + 0 = 0, 1 + 0 = 1, 0 + 1 = 1, 1 + 1 = 10 (carry the 1). Therefore we can use the bitwise XOR operator (^) when iterating through the digits, taking into account whether we are carrying a 1 from the previous digit addition. For example 
Fractional Parts: 
:
|
1 2 3 4 5 6 7 8 |
// Iterate through the characters from right to left, matching up the beginning (lhs) of both strings for (auto i = length - 1; i >= 0; --i) { const auto leftChar = (i >= leftLength) ? '0' : left[i]; const auto rightChar = (i >= rightLength) ? '0' : right[i]; result[i] = '0' + ((carry) ? (1 ^ leftChar ^ rightChar) : (leftChar ^ rightChar)); carry = (carry) ? ((leftChar | rightChar) == '1') : ((leftChar & rightChar) == '1'); } |
Integer Parts: 
:
|
1 2 3 4 5 6 7 8 |
// Iterate through the characters from right to left, matching up the end (rhs) of both strings for (int l = leftLength - 1, r = rightLength - 1, i = length - 1; i >= 0; --l, --r, --i) { const auto leftChar = (l < 0) ? '0' : left[l]; const auto rightChar = (r < 0) ? '0' : right[r]; result[i] = '0' + ((carry) ? (1 ^ leftChar ^ rightChar) : (leftChar ^ rightChar)); carry = (carry) ? (('1' & (leftChar | rightChar)) == '1') : ((leftChar & rightChar) == '1'); } |
Subtraction
For binary subtraction the rules are: 0 – 0 = 0, 1 – 0 = 1, 0 – 1 = 1 (1 borrowed from next digit on top), 1 – 1 = 0. In order to simplify the subtraction logic, the largest value is on the left hand side of the – operator and the smallest value is on the right hand side. After the calculation is complete the result is negated if required. Only when the top digit is 0 and the bottom digit is 1 do we need to borrow. The bitwise XOR operator (^) can be used in the other situations. For example 
Fractional Parts: 
:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
// Iterate through the characters from right to left, matching up the beginning (lhs) of both strings for (auto i = length - 1; i >= 0; --i) { const auto leftChar = (i >= leftLength) ? '0' : topInteger[i]; const auto rightChar = (i >= rightLength) ? '0' : right[i]; if (leftChar == '0' && rightChar == '1') { if (!borrowOnes(topInteger, i)) borrow = true; result[i] = '1'; } else { result[i] = '0' + (leftChar ^ rightChar); } } |
Integer Parts: 
:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
// Iterate through the characters from right to left, matching up the end (rhs) of both strings for (auto l = leftLength - 1, r = rightLength - 1, i = length - 1; i >= 0; --l, --r, --i) { const auto leftChar = (l < 0) ? '0' : topInteger[l]; const auto rightChar = (r < 0) ? '0' : right[r]; if (leftChar == '0' && rightChar == '1') { borrowOnes(topInteger, l); result[i] = '1'; } else { result[i] = '0' + (leftChar ^ rightChar); } } |
Summary
While using strings to demonstrate addition and subtraction isn’t the most optimal solution, it is a good way to visualize the operations. In the next post I will cover multiplication and division as well as providing a link to the code.
Hi there,
Nice article, I use it to understand floating point mathematics, but I found error here. When you convert exponent 130 to binary representation you got somehow 10000011, however 130 is 10000010. As result 12.125 representation is 01000001010000100000000000000000. You picture here http://www.eoinoflynn.com/wp-content/uploads/2015/02/binary_float.png is representation of 24.25 decimal. Please correct me if I wrong.
Just in case: I use also this to check results http://www.h-schmidt.net/FloatConverter/IEEE754.html
Hi Alezis,
Thanks for your comment and for pointing out my error. You are absolutely right and I will update the diagram and the calculations with your correction.
Eóin